利用与探索的权衡
利用与探索的困境存在于我们生活的许多方面。例如,你最喜欢的餐馆就在拐角处。如果你每天去那里,你会知道自己能得到什么,但错过了发现更好的机会。如果你总是尝试新地方,很可能你会经常吃到不太好吃的食物。类似地,在线广告商也试图平衡已知的最吸引人的广告和可能更成功的新广告。
图1. 探索与探索困境的现实例子:去哪儿吃饭?(图片来源:UC Berkeley AI课程 幻灯片,Lecture 11)
如果我们已经了解了环境的所有信息,我们甚至可以通过模拟暴力搜索来找到最好的策略,更不用说其他智能方法了。困境来自于不完整的信息:我们需要收集足够的信息以做出最佳的整体决策,同时控制风险。通过开发,我们利用我们知道的最佳选择。通过探索,我们冒险收集关于未知选项的信息。最佳的长期策略可能涉及短期的牺牲。例如,一次探索实验可能会完全失败,但它警告我们未来不要过于频繁地采取该行动。
什么是多臂赌博机?
多臂赌博机问题是一个经典问题,能很好地展示开发与探索的困境。想象一下,你在一个赌场里,面对多个老虎机,每个老虎机都有一个未知的概率,表示你在一次游戏中获得奖励的可能性。问题是:如何才能制定最佳策略,以获得最高的长期回报?
在这篇文章中,我们只讨论无限次试验的情况。有限次数试验的限制引入了一种新的探索问题。例如,如果试验次数小于老虎机的数量,我们甚至无法尝试每个机器来估算奖励概率(!),因此我们必须在有限的知识和资源(例如时间)下聪明地行动。
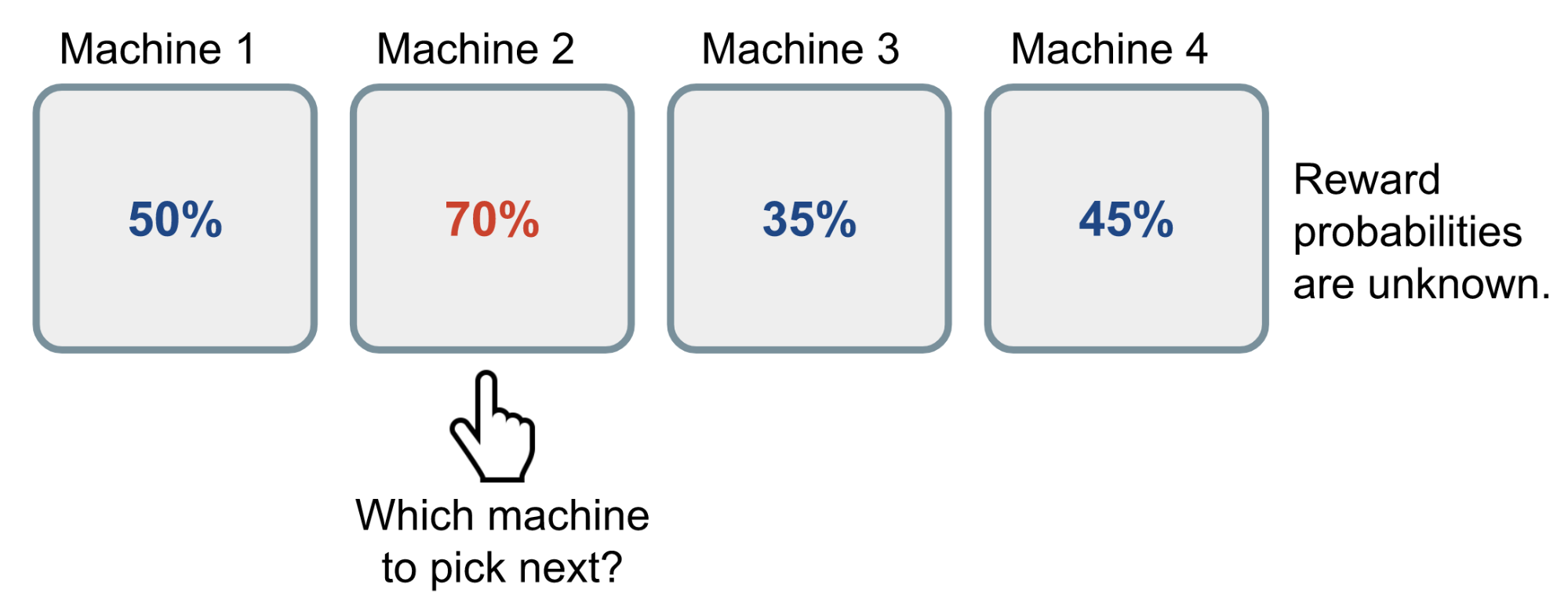
图2. 伯努利多臂赌博机的工作原理。奖励概率对于玩家来说是未知的。
一个简单的方法是你继续玩一个机器很多轮,最终通过大数法则估计“真实”奖励概率。然而,这种方法非常浪费,并且并不能保证获得最佳的长期回报。
定义
现在我们给出科学的定义。
一个伯努利多臂赌博机可以描述为一个元组 \(\langle \mathcal{A}, \mathcal{R} \rangle\),其中:
- 我们有 $K$ 个机器,每个机器的奖励概率为 ${\theta_1, \dots, \theta_K}$。
- 在每个时间步 $t$,我们对一个老虎机采取动作 $a$ 并获得奖励 $r$。
- $\mathcal{A}$ 是一个动作集,每个动作指代与一个老虎机的交互。动作 $a$ 的值是预期奖励,
如果时间步 $t$ 的动作 $a_t$ 在第 $i$ 个机器上,那么 $Q(a_t) = \theta_i$。
- $\mathcal{R}$ 是奖励函数。在伯努利赌博机的情况下,我们以随机的方式观察奖励 $r$。在时间步 $t$,$r_t = \mathcal{R}(a_t)$ 可能以概率 $Q(a_t)$ 返回奖励 1,或者返回 0。
它是马尔可夫决策过程的简化版本,因为没有状态 $\mathcal{S}$。
目标是最大化累积奖励 $\sum_{t=1}^T r_t$。如果我们知道最优动作对应的最佳奖励,那么目标就是最小化由于没有选择最佳动作而可能产生的后悔或损失。
最优奖励概率 $\theta^{*}$ 对应最优动作 $a^{*}$ 是:
\[\theta^{*} = Q(a^{*}) = \max_{a \in \mathcal{A}} Q(a) = \max_{1 \leq i \leq K} \theta_i\]我们的损失函数是我们未选择最佳动作而造成的总后悔:
\[\mathcal{L}_T = \mathbb{E} \left[ \sum_{t=1}^T (\theta^{*} - Q(a_t)) \right]\]赌博机策略
根据我们如何进行探索,有几种方法可以解决多臂赌博机问题。
- 不进行探索:最简单的方式,但效果很差。
- 随机探索
- 智能探索,优先考虑不确定性较高的选项
ε-贪婪算法
ε-贪婪算法大多数时候选择最好的动作,但偶尔会进行随机探索。动作值根据过去的经验进行估计,方法是平均已观察到的目标动作 $a$ 的奖励(直到当前时间步 $t$):
\[\hat{Q}_t(a) = \frac{1}{N_t(a)} \sum_{\tau=1}^t r_\tau \mathbb{1}[a_\tau = a]\]其中,$\mathbb{1}$ 是二进制指示函数,$N_t(a)$ 表示动作 $a$ 已经被选择的次数,$N_t(a) = \sum_{\tau=1}^t \mathbb{1}[a_\tau = a]$。
根据ε-贪婪算法,给定小概率 $\epsilon$,我们会随机选择一个动作;但大多数时间(即概率为 $1-\epsilon$),我们选择我们目前学到的最好的动作:
\[\hat{a}^{*}_t = \arg\max_{a \in \mathcal{A}} \hat{Q}_t(a)\]你可以查看我的玩具实现。
上置信区间
随机探索给我们一个机会去尝试那些我们之前不太了解的选项。然而,由于随机性,我们有可能探索到一个我们之前确认过的糟糕动作(运气不好!)。为了避免这种低效的探索,一种方法是随时间逐渐减少参数 $\epsilon$,另一种方法是对那些具有高不确定性的选项持乐观态度,优先选择我们还没有足够信心估计的动作。换句话说,我们偏向于探索那些可能具有最佳价值的动作。
上置信区间(UCB)算法通过一个奖励值的上置信区间来衡量这个潜力,$\hat{U}_t(a)$,这样真实值就会以较高的概率低于上界,即 $Q(a) \leq \hat{Q}_t(a) + \hat{U}_t(a)$。
UCB算法中,我们始终选择最贪婪的动作来最大化上置信区间:
\[a_t^{UCB} = \arg\max_{a \in \mathcal{A}} \left( Q(a) + \hat{U}_t(a) \right)\]现在,问题是如何估计上置信区间。
Hoeffding不等式
如果我们不想对分布的形状进行任何先验假设,可以借助Hoeffding不等式——一个适用于任何有界分布的定理。
让 $X_1, \dots, X_t$ 是独立同分布(i.i.d.)的随机变量,它们都被限制在区间 $[0, 1]$ 内。样本均值为 $\overline{X}t = \frac{1}{t} \sum{\tau=1}^t X_\tau$。然后对于 $u > 0$,我们有:
\[\mathbb{P} \left[ \mathbb{E}[X] > \overline{X}_t + u \right] \leq e^{-2tu^2}\]给定一个目标动作 $a$,考虑:
- $r_t(a)$ 为随机变量,
- $Q(a)$ 为真实均值,
- $\hat{Q}_t(a)$ 为样本均值,
- $u$ 为上置信区间,$u = U_t(a)$
然后我们有:
\[\mathbb{P} \left[ Q(a) > \hat{Q}_t(a) + U_t(a) \right] \leq e^{-2t U_t(a)^2}\]我们希望选择一个上界,使得以较高的概率真实均值会小于样本均值+上置信区间。我们设定阈值 $p$ 为一个小概率:
\[e^{-2t U_t(a)^2} = p \quad \Rightarrow \quad U_t(a) = \sqrt{-\frac{\log p}{2 t N_t(a)}}\]UCB1
一种启发式方法是随时间减少阈值 $p$,因为我们希望通过观察更多的奖励来做出更可信的界限估计。当我们设定 $p = t^{-4}$ 时,我们得到 UCB1 算法:
\[U_t(a) = \sqrt{\frac{2 \log t}{N_t(a)}} \quad \text{and} \quad a_t^{UCB1} = \arg\max_{a \in \mathcal{A}} \left( Q(a) + \sqrt{\frac{2 \log t}{N_t(a)}} \right)\]贝叶斯UCB
在UCB或UCB1算法中,我们没有假设奖励分布的任何先验,因此必须依赖Hoeffding不等式来做一个非常广泛的估计。如果我们能够预先知道分布,我们就能做出更好的界限估计。
例如,如果我们预计每个老虎机的平均奖励呈高斯分布,如图2所示,我们可以通过设置 $U_t(a)$ 为两倍标准差,来设定上界为95%的置信区间。
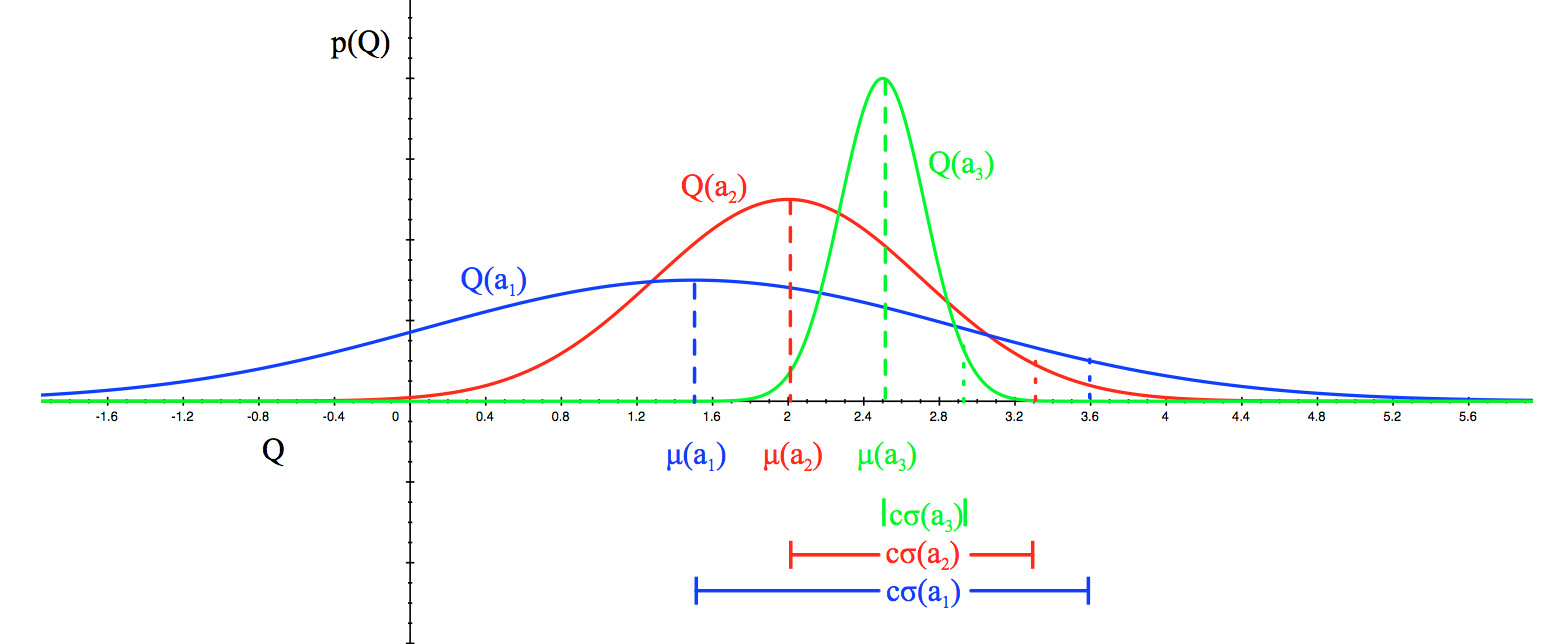
图3. 当期望奖励有高斯分布时。$\sigma(a_i)$ 为标准差,$c\sigma(a_i)$ 为上置信区间。常数 $c$ 是一个可调超参数。(图片来源:UCL RL课程第9讲幻灯片)
汤普森采样
汤普森采样有一个简单的思想,但在解决多臂赌博机问题时效果非常好。

图4. 哎呀,我猜这不是汤普森?(感谢Ben Taborsky,他有一个关于汤普森发明这个算法的完整定理。是的,我偷了他的笑话。)
在每个时间步,我们根据某个动作最优的概率选择动作a:
\[\pi(a|h_t) = \mathbb{P} \left[ Q(a) > Q(a'), \forall a' \neq a | h_t \right] = \mathbb{E}[R|h_t] \mathbb{1}(a = \arg\max_{a \in \mathcal{A}} Q(a))\]其中,
\[\pi(a|h_t)\]是给定历史 $h_t$ 选择动作 $a$ 的概率。
对于伯努利赌博机,假设 $Q(a)$ 遵循Beta分布是很自然的,因为 $Q(a)$ 本质上是伯努利分布中的成功概率 $\theta$。Beta(α,β)的值在区间 $[0, 1]$ 内;α 和 β 分别对应我们成功和失败获得奖励的次数。
首先,我们基于某些先验知识或信念初始化每个动作的 Beta 参数 α 和 β。例如,
- α = 1, β = 1;我们预计奖励概率为50%,但信心不大。
- α = 1000, β = 9000;我们坚信奖励概率为10%。
每个时间 $t$,我们从每个动作的先验分布 Beta(α_i, β_i) 中采样一个期望奖励 $Q(a)$。最佳动作是在这些样本中选择的:$a_t^{TS} = \arg\max_{a \in \mathcal{A}} Q(a)$。在观察到真实奖励后,我们可以相应地更新 Beta 分布,这本质上是在进行贝叶斯推断,计算已知先验和样本数据的后验分布。
\[\alpha_i \leftarrow \alpha_i + r_t \mathbb{1}[a_t^{TS} = a_i] \quad \beta_i \leftarrow \beta_i + (1 - r_t) \mathbb{1}[a_t^{TS} = a_i]\]汤普森采样实现了概率匹配的思想。因为它的奖励估计 $Q$ 是从后验分布中采样的,所以这些概率与相应动作是最优的概率是等价的,条件是观察到的历史。
然而,对于许多实际和复杂的问题,通过贝叶斯推断估计后验分布会计算上不可行。如果我们能够使用吉布斯采样、拉普拉斯近似、引导法等方法来近似后验分布,汤普森采样仍然可以有效工作。这篇教程提供了全面的回顾;如果你想深入了解汤普森采样,强烈推荐它。
案例研究
我在lilianweng/multi-armed-bandit中实现了上述算法。可以通过一个随机或预定义奖励概率列表构造一个BernoulliBandit对象。赌博机算法作为Solver的子类实现,接受Bandit对象作为目标问题。累积后悔随着时间跟踪。
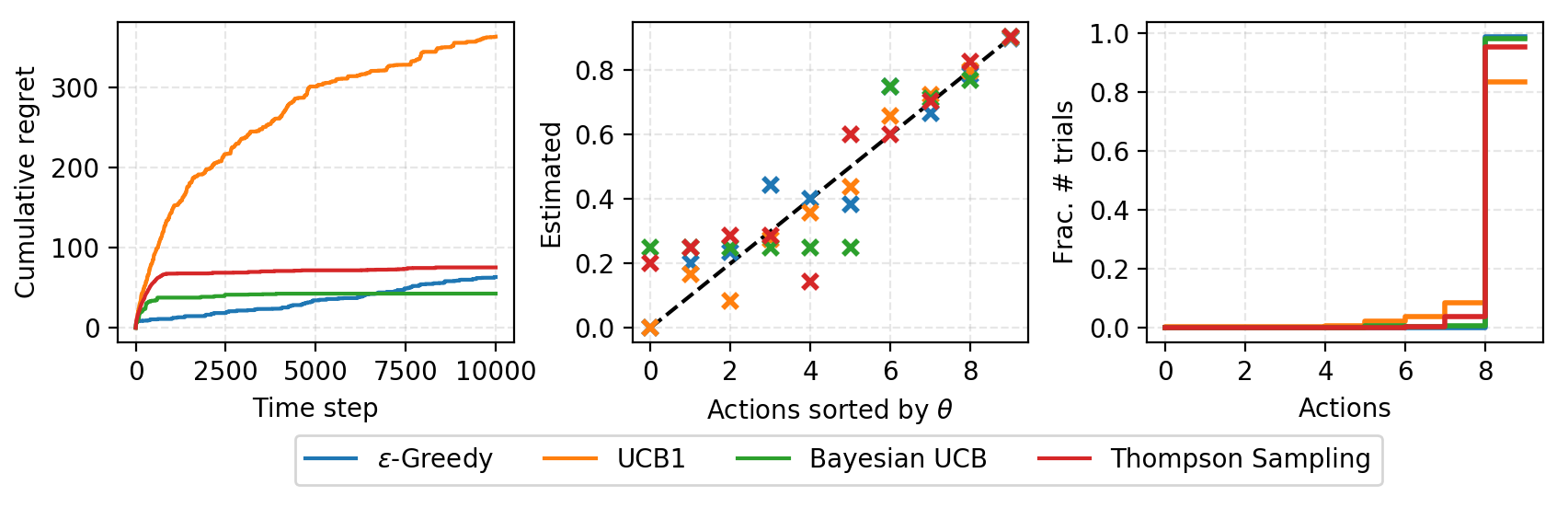
图4. 解决伯努利赌博机的小实验结果,K = 10个老虎机,奖励概率为{0.0, 0.1, 0.2, …, 0.9}。每个求解器运行10000步。
(左) 时间步与累计后悔的图;(中) 真实奖励概率与估计概率的图;(右) 每个动作在10000步中的选择比例。
总结
我们需要探索,因为信息是有价值的。就探索策略而言,我们可以选择完全不探索,专注于短期回报;或者偶尔随机探索;更进一步,我们可以探索,并挑选出哪些选项值得探索——那些不确定性较高的动作更受青睐,因为它们能够提供更高的信息增益。

参考
[1] 翻译自:The Multi-Armed Bandit Problem and Its Solutions
[2] 多臂老虎机beta分布与汤姆森采样参考:小孩都看得懂的多臂老虎机和汤姆森采样
[3] PR Reasoning Ⅱ:Bandit问题与 UCB / UCT / AlphaGo.
您的打赏是对我最大的鼓励!
 支付宝打赏
支付宝打赏  微信打赏
微信打赏